在学习三角函数时,倍角公式和半角公式是经常用到的两种重要公式。然而,由于这两种公式涉及的数学知识较多,记忆起来比较困难。为了帮助大家更好地记忆这两种公式,本文将介绍一种简便方法口诀。
一、倍角公式口诀
倍角公式是用来计算一个角度的两倍值的三角函数值的公式。主要包括正弦倍角公式、余弦倍角公式和正切倍角公式。这里我们给出一个口诀来帮助记忆这三种公式:
正弦倍角:Sin2x = 2SinxCosx;
余弦倍角:Cos2x = Cos²x - Sin²x;
正切倍角:Tan2x = 2Tanx / (1 - Tan²x)。
通过这个口诀,我们可以快速地写出倍角公式,提高解题效率。
二、半角公式口诀
半角公式是用来计算一个角度的一半值的三角函数值的公式。同样包括正弦半角公式、余弦半角公式和正切半角公式。我们也给出一个口诀来帮助记忆这三种公式:
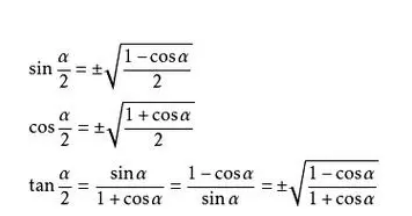
正弦半角:Sin^2(x/2) = (1 - Cosx) / 2;
余弦半角:Cos^2(x/2) = (1 + Cosx) / 2;
正切半角:Tan(x/2) = Sinx / (1 + Cosx)。
通过这个口诀,我们可以快速地写出半角公式,提高解题效率。
三、运用口诀进行实际计算
掌握了倍角和半角公式的口诀后,我们需要学会如何运用这些口诀进行实际计算。在解决具体问题时,我们可以根据题目给出的条件和要求,灵活运用这些口诀来简化计算过程,提高解题速度。
例如,在求解一个三角函数方程时,我们可以先观察方程的形式,判断是否可以运用倍角或半角公式进行化简。如果可以,那么就可以直接运用相应的口诀进行计算,从而简化问题。
结语:
总之,倍角半角公式的简便方法口诀是一种非常实用的技巧,可以帮助我们快速记忆和运用这两种公式。通过熟练掌握这些口诀,并在实际问题中灵活运用,我们可以大大提高解题效率,更好地应对各种三角函数问题。









