祖暅原理及其在古代数学中的应用
祖暅原理，源于中国古代数学家祖暅对几何学的研究，是中国古代数学史上的一项杰出成就。这一原理不仅在当时的数学研究中具有重要地位，而且对后世数学的发展产生了深远的影响。本文将探讨祖暅原理的基本内容及其在古代数学中的应用。
祖暅原理，简单来说，是关于几何图形的切割和组合的原理。它指出，两个等高的立体图形，如果它们的底面积相等，那么它们的体积也相等。这一原理在古代数学中被广泛应用于求解各种几何体的长度、面积和体积问题。
在古代数学中，祖暅原理的应用非常广泛。例如，在求解圆柱体、圆锥体和球体的体积时，古代数学家就运用了这一原理。通过将复杂的几何体切割成若干个简单的几何体，然后根据祖暅原理进行组合，可以方便地求解出这些几何体的体积。
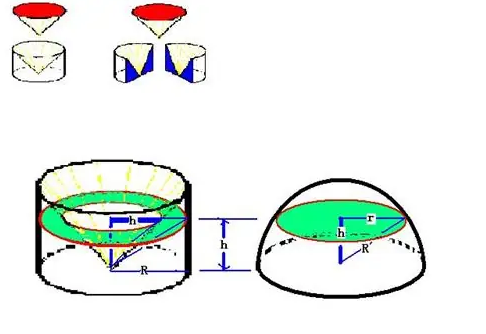
此外，祖暅原理还被用于解决一些实际问题。比如，在古代的建筑和水利工程中，需要计算各种形状的材料的体积。这时，祖暅原理就发挥了重要作用。通过应用这一原理，工程师可以快速准确地计算出所需材料的数量，从而提高工程效率。
值得一提的是，祖暅原理在古代数学中的地位并不仅仅局限于几何学领域。事实上，它与当时的代数学、方程论等领域也有密切的联系。许多复杂的数学问题都可以通过祖暅原理转化为简单的几何问题来解决。因此，祖暅原理被认为是古代数学中的一个基本工具和方法。
免责声明：以上内容源自网络，版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。
